Perceptron
McCulloch-Pitts Neuron Model


- 출력 Binary
- 수상 돌기에 도착한 여러 신호가 세포체에 합쳐짐
- 합쳐진 신호가 특정 값을 넘으면 축삭 돌기를 이용하여 출력 신호 전달
>> 몇 년 후 MCP Neural Model 기반의 Perceptron 등장
Perceptron
- 이진 분류에 적용 가능
- Positive Class: +1
- Negative Class: -1
- 선형적으로 구분 가능한 데이터에 대해 사용 (그렇지 않을 경우 Updqte가 멈추지 않음)
결정 함수
$$
\phi(z) = \phi(w^Tx)
$$

- z값이 Threshold $\tau$에 따라 Positive Negative 판별
학습 규칙

|
(예시)
$$
\Delta w_0=\eta(y^{(i)}-output^{(i)})\\
\Delta w_1=\eta(y^{(i)}-output^{(i)})x_1^{(i)}\\
\Delta w_2=\eta(y^{(i)}-output^{(i)})x_2^{(i)}
$$
보완
Net input function 결과가 $\tau = 0$ 일 경우 0.01이든 0.99이든 결과값이 1이지만 오차값을 계산할 필요가 있음
>> 진짜 1인지를 확인해야 함
Adaptive Linear Neuron

가중치 업데이트를 위해 Step Function이 아닌 Linear Activation Function을 사용
- Class Label과 실수 출력 값을 비교하여 오차 계산
실제값과 예측값의 차이가 있으면 경사하강법으로 가중치 업데이트- 미분 가능한 비용 함수
- Gradient Descent 이용 가능
>> Activation function에 대한 이해
Multi-Layer Perceptron
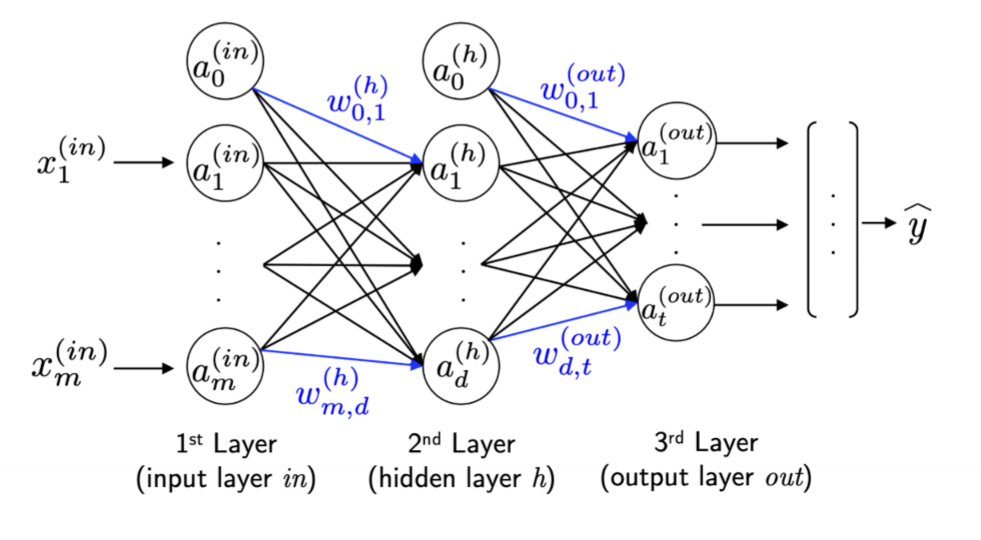
Perceptron이 Non-Linear한 데이터를 분류하지 못하는 문제를 해결
The equations of backpropagation
$$
\delta^L = \nabla_aC \,\odot\, \sigma^\prime(z^\prime)\\
\,\\
\delta^l = ((w^{l+1})^T\delta^{l+1})\,\odot\,\sigma^\prime(z^l)\\
\,\\
{\frac{\partial C}{\partial b_j^l} = \delta_j^l}\\
\, \\
{\frac{\partial C}{\partial w_{jk}^l} = a_k^{l-1}\delta_j^l}
$$
(유도는 공부하면서 다시 정리)
'Computer Science > 머신러닝' 카테고리의 다른 글
| 머신러닝:: Ensemble Learning (0) | 2023.06.11 |
|---|---|
| 머신러닝:: Dimensionality Reduction (0) | 2023.06.11 |
| 머신러닝:: Regularization (0) | 2023.06.08 |
| 머신러닝:: Clustering (0) | 2023.06.06 |
