Instance-Based Learning
Nonparametric model
고정된 크기의 parameter set으로 데이터를 특징화할 수 없을 때 사용하는 모델
- 학습된 사례들을 기억하는 것으로, 시스템이 훈련 데이터를 기억함으로써 학습한다.
- 새로운 데이터가 들어오는 경우, 학습된 데이터(일부 또는 전체)와 새로운 데이터의 유사도를 측정하여, 입력된 새로운 데이터를 가장 유사도가 높은 기존 학습 데이터의 클래스로 분류한다.
- 새로운 데이터가 들어오기 전까지 계산을 미루기 때문에 'lazy' algorithm 이라고 부르기도 한다.
Parametric model
고정된 크기의 parameter set을 데이터와 함께 추출한 모델
Model-based learning
데이터 셋에 적합한 모델을 사용하여 모델을 만들고, 모델을 이용하여 새로운 데이터를 어떻게 분류할지 예측(Prediction)한다.
KNN
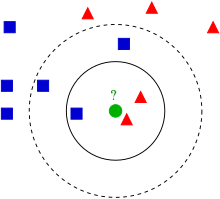
$x_q$에 대해서 가장 가까운 neighbor를 찾는 방식 ($NN(k, x_q)$)
- Classification : voting (결과값 중 최빈값)
- Regression : 결과값의 mean 혹은 median
Curse of Dimensionality

차원이 커질 수록 nearest neighbor가 near하지 않다.
-> 차원이 커질 수록 데이터 사이의 거리가 멀어지고, 빈공간이 증가하면서 데이터가 희소해진다.
증명
$k$ : neighbor 수
$l$ : neighbor 사이의 평균 거리
$l^n$ : neighbor 수
$n$ : $n$차원
$N$ : $1^n$ 부피의 큐브 안에 균일하게 분포된 점의 개수
$$
{l^n \over 1^n} = l^n = {k \over N} \Leftrightarrow l = \big({k \over N}\big)^ {1 \over n}
$$
neareast와 point의 개수가 동일할 때,
- $n=3 \longrightarrow l=0.02$
- $n=17 \longrightarrow l=0.5$
- $n=200 \longrightarrow l=0.94$
차원이 커질 수록 neighbor 사이의 평균 거리가 길어짐을 알 수 있다.
Distance Functions
- $L^p ,norm$
$$
L^p(x_j, x_q) = \big(\sum_i\big|x_{j, i} - x_{q, i}\big|^p\big)^{1 \over p}
$$- $p = 2$: Euclidean distance
- $p = 1$: Manhatten distance
- $p = 1$ with Boolean attributes: Haming distanc
- Normalization / Standardization
벡터의 크기를 고려하지 않아 특정 attribute의 영향력이 커지게 되는 문제를 해결하기 위한 방법- min-max Normalization
$$
a_i={{v_i - \min v_i}\over {\max v_i - \min v_i}}\
,\
(v_i: \text{actual value of attribute }i)
$$
모든 feature에 대해 각각의 최솟값으로 0, 최대값을 1로, 그리고 다른 값들은 0~1 사이의 값으로 변환하는 방법장점: 모든 feature의 스케일 동일단점: 이상치에 많은 영향을 받음
- Z-score Standardization
$$
x_{j, i} \rightarrow {(x_{j, i} - \mu_i)\over \sigma_i}
$$
Z-score 공식을 이용해 변환하는 방법장점: 이상치 문제를 피할 수 있음단점: 정확히 동일한 척도로 정규화된 데이터를 생성하진 않음
- min-max Normalization
Nearest Neighbors를 효과적으로 찾기
- kD-tree
k 차원으로 구성된 balanced binary tree- left and right subtrees의 높이 차 $\le$ 1
- left and right subtrees도 balanced 해야 한다.
- kD-tree 만드는 방법
- 분산이 최고치가 되는 차원을 고른다.
- 중앙값을 고르고 그 점을 기준으로 나눈다.
- 위 과정을 반복한다.
예제


Clustering
- Unsupervised Learning (비지도 학습, 라벨이 없음)
- 클러스터는 비슷한 샘플로 구성 됨
- 같은 클러스터 - 유사도 높음
- 다른 클러스터 - 유사도 낮음
- 분류 기준
- Disjoint vs Overlapping

Disjoint vs Overlapping - Deterministic vs Probabilistic

Probabilistic - Hierarchical vs Flat

Hierarchical
- Disjoint vs Overlapping
$k$-means algorithm

- 특징 : Disjoint / Statistical (Probabilistic) / Hierarchical
- k에 따라 성능이 결정됨
과정
k개의 cluster를 만든다고 가정하자
- 각 cluster에 임의의 center point를 지정
- 각 instance와 center와의 거리를 구한 후, instance와 가장 가까운 center를 지정
- instance를 바탕으로 centroid 업데이트
- center가 바뀌지 않을 때까지 각 cluster의 center 갱신
[Squared Euclidean Distance]
$$
d(x, y)^2 = \sum_{j=1}^m(x_j - y_j)^2 = \big|\big|x-y\big|\big|_2^2\
x, y \in \mathbb{R}^m
$$
조건 : 모든 점과 cluster의 center와의 Squared Euclidean Distance의 합이 최소화되도록 해야 함
한계
- local optima의 문제
초기 center에 따라 cluster가 달라질 수 있음
$$
SSE = \sum_{i=1}^n\sum_{j=1}^kw^{(i, j)}\big|\big| x^{(i)} - {\mu}^{(j)} \big|\big|_2^2\
,\
w^{(i, j)} \text{: 샘플 i의 Cluster j 소속 여부}, \mu^j \text{: Cluster j의 Centroid}
$$
-> 초기 값을 바꿔가면서 Sum of Squared Errors (SSE)가 최소가 되도록 해야 함
$k$-means++ Clustering
한계
- k개의 Centroid를 저장할 집합 $M$ 초기화
- 데이터에서 첫 번째 Centroid $\mu^i$를 Random하게 선택하여 $M$에 추가
- $M$의 원소가 아닌 각 샘플 $x^i$에 대해 $M$에 있는 Centroid까지의 최소 제곱 거리 $d(x^i, M)^2$를 계산
- 다음과 같은 가중치가 적용된 확률 분포를 사용하여 다음 Centroid $\mu^p$를 Random하게 선택
$$
{{d(\mu^p, M)^2} \over {\sum_i d(x^i, M)^2}}=
{\text{특정 sample 거리 } \over \text{모든 sample 거리 합}}
$$ - k개의 Centroid를 선택할 때까지 반복
- 기본 k-means Clustering 수행
'Computer Science > 머신러닝' 카테고리의 다른 글
| 머신러닝:: Multi-Layer Perceptron(MLP) (1) | 2023.06.12 |
|---|---|
| 머신러닝:: Ensemble Learning (0) | 2023.06.11 |
| 머신러닝:: Dimensionality Reduction (0) | 2023.06.11 |
| 머신러닝:: Regularization (0) | 2023.06.08 |
