Image Resizing
Resizing이 필요한 이유
컴퓨터에게 물체를 인식하는데 필요하기 때문이다.
같은 자동차라고 할지라도 거리에 따라 컴퓨터는 인식을 다르게 할 수 있다.
따라서 컴퓨터가 제대로 인식하기 위해서는 Resizing을 생각해볼 필요가 있다.
Image Sub-sampling
문제
이미지를 Sub-sampling하면 픽셀이 날라가면서 화질이 감소하거나 이미지가 왜곡되는 문제점이 생길 수 있다.
Aliasing (위신호 현상, 계단 현상)
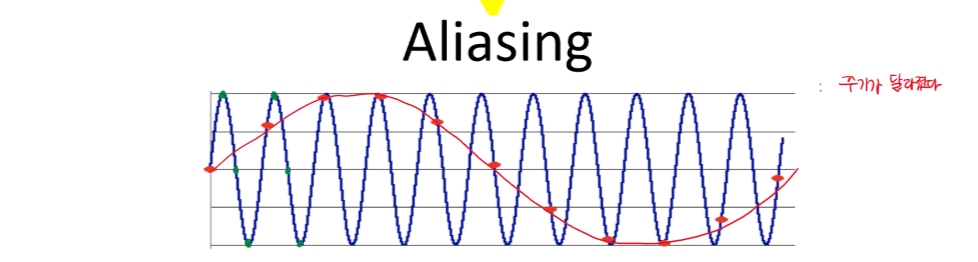
sampling rate가 원본 이미지를 복원할 정도로 충분히 높지 않기 때문에 발생한다.

샘플링 후 신호를 복원하게 되면 원래 신호와 주파수가 달라지게 되어 원래 신호를 복원하지 못하는 문제 생긴다.
이에 대한 이유는 위해서 말했다시피 적절한 속도로 샘플링하지 않았기 때문이다.
Aliasing을 피하는 방법
sampling rate를 높이자 > 얼마만큼 높이는데? > Nyquist rate 공식에 의해 sampling rate를 결정하자!
Nyquist rate
Aliasing을 피하는데 최소한의 sampling rate 공식
sampling rate >= 2 * max frequency
한계

단, sampling이 고르지 않을 경우 Nyquist 공식에 의한 sample rate도 원본 이미지를 복원하는데 충분하지 않을 수 있음
Image Pre-Filtering
이미지는 high frequency와 low frequency로 구성되어 있다.
- high frequency components : pixel to pixel detail
- low frequency components : high-level structure
자세한 디테일보다는 전체적인 구조를 챙겨가기 위해
pixel to pixel detail 즉, high frequency components를 제거함으로써
high-level structure 즉, low frequency components를 남기는 방식을 사용할 것이다.
Gaussian pre-filtering
low-pass filter를 통해 high requency를 제거하는 방법


Upsampling
- 이미지를 upsample한 후, 값을 0으로 채운다 (upsample and fill with 0s)
- 가우시안 필터 적용 (Gaussian blur to interpolate)
- 1단계 0으로 채운 부분을 보정 (Scale correction) - interpolation
Laplacian pyramid
원본 이미지를 얻기 위해서는 현재 이미지 단계에서 한 단계 위의 이미지 정보가 필요하다.
원본 이미지보다 높은 주파수는 어떻게 얻을까? > Gaussian Filter를 응용해보자!
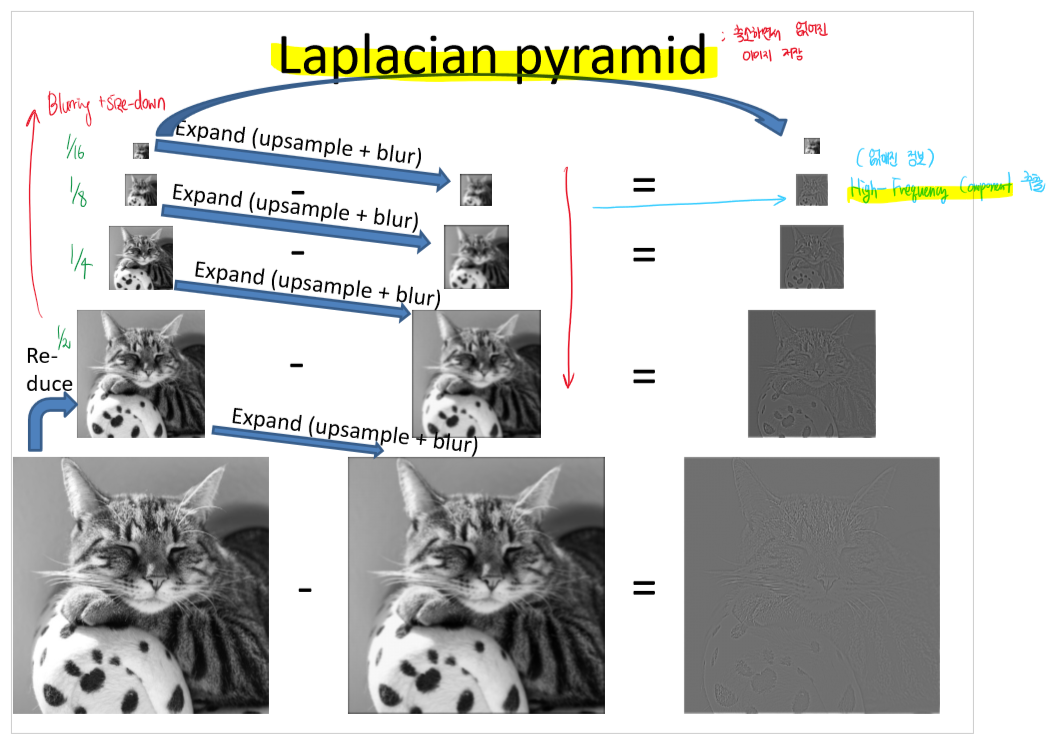
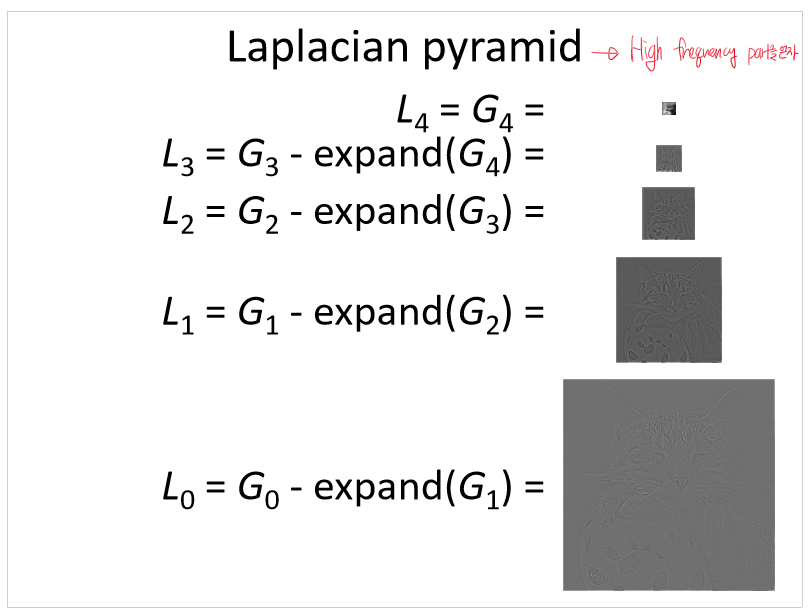
Laplacian pyramid로 이미지 resampling

Image interpolation
현재 알고 있는 sample을 통해 모르는 sample을 구하고 싶다.
함수 f를 통해 sample을 구할 수 있다.
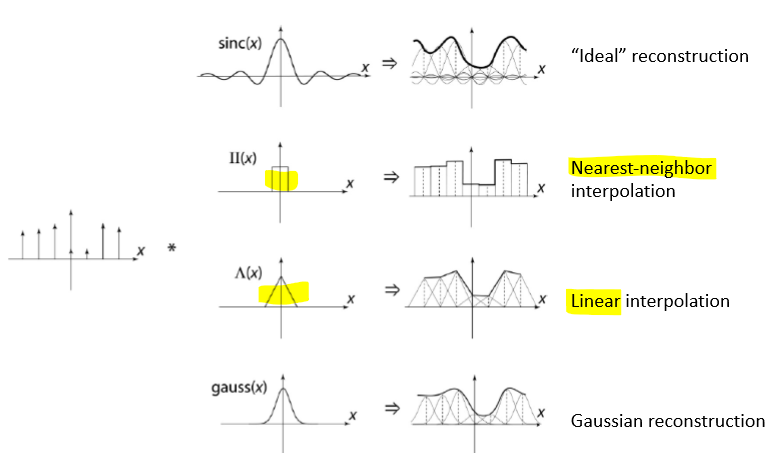
예시

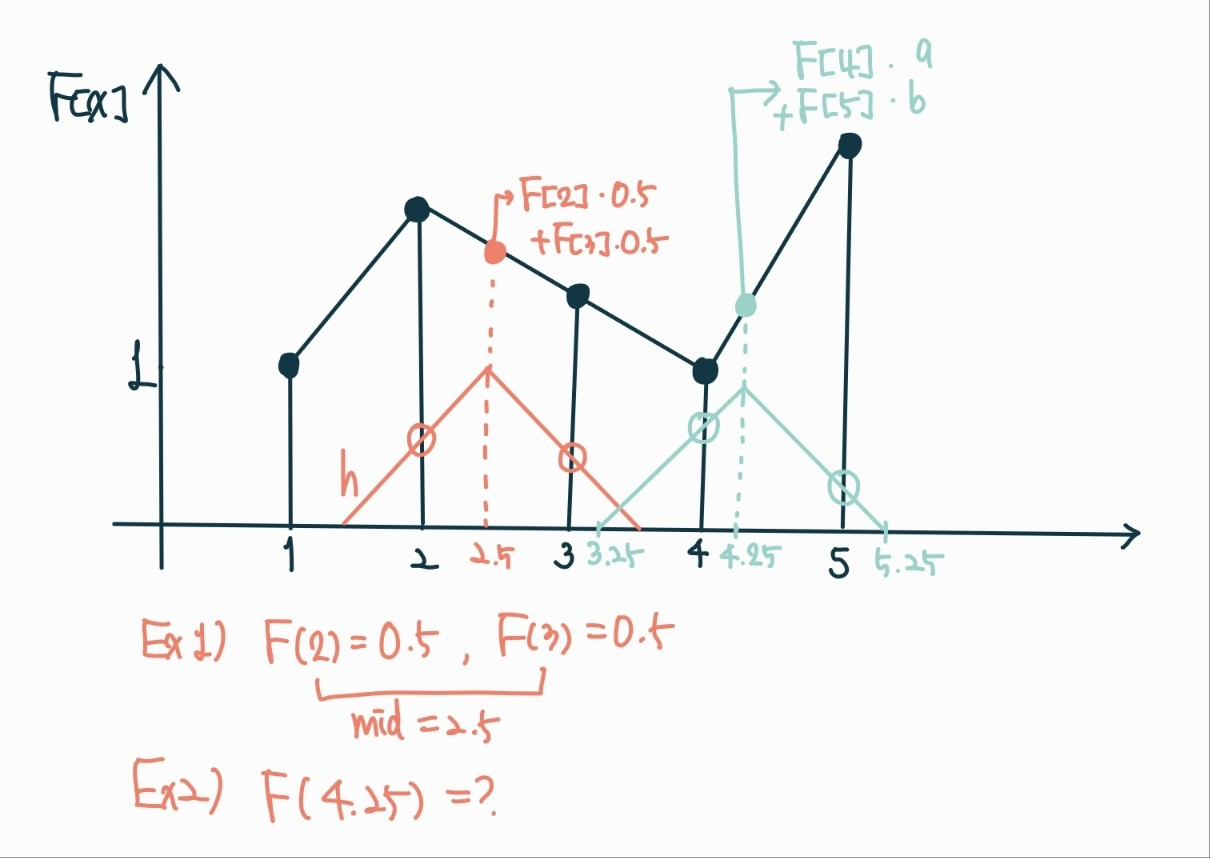
linear kernel이기 때문에 결과가 직선으로 나온다.
(기울기 개념으로 생각하면 계산하기 편할거 같다)
참고

Nearest-neighbor - 이미지가 많이 깨짐
Bilinear - edge에서 불연속한 부분이 보임
Bicubic - edge가 좀 더 부드럽게 보임
이외 고화질 사진을 위해 여러 기술들이 연구되고 있다.
Hybrid Image

Image 사이즈가 클 때는 high frequency components가 도드라져 보이고
Image 사이즈가 작을 때는 low frequency components가 도드라져 보이는 Image
즉, 하나의 Image에 high frequency, low frequency components가 같이 있는 Image
'Computer Science > 컴퓨터비전' 카테고리의 다른 글
| 컴퓨터비전:: Transformation & Warping (0) | 2023.04.13 |
|---|---|
| 컴퓨터비전:: Image Descriptors & Match (0) | 2023.04.12 |
| 컴퓨터비전:: Harris corner detection (0) | 2023.04.12 |
| 컴퓨터비전:: Edge & Edge Detection (0) | 2023.03.15 |
| 컴퓨터 비전:: Image Filtering (0) | 2023.03.15 |
