파노라마 사진 만들기
1. feature
1) 특징 찾기 - local feature : corner
2) 특징 묘사 - vector로 표시
3) 특징끼리 연결 (match)
2. alignment
1) transform & warping
2) alignment
이전 포스팅에서는 warping을 위한 여러가지 transformation matrix에 대해 알아보았다.
이번에는 transformation matrix를 구하는 방법에 대해 알아보고자 한다.
Image alignment
Image alignment 알고리즘
1. A와 B의 image feature 구하기
2. A와 B feature 매칭하기
3. Least square를 통해 A와 B사이의 homography 계산하기
4. Image warping
앞서 feature를 구하고 descriptor을 정의하여 이것들을 매칭하였다.
매칭 후 이들간의 transformation에 대해 구하여 가장 적합한 transformation matrix를 찾아보려고 한다.
Translation
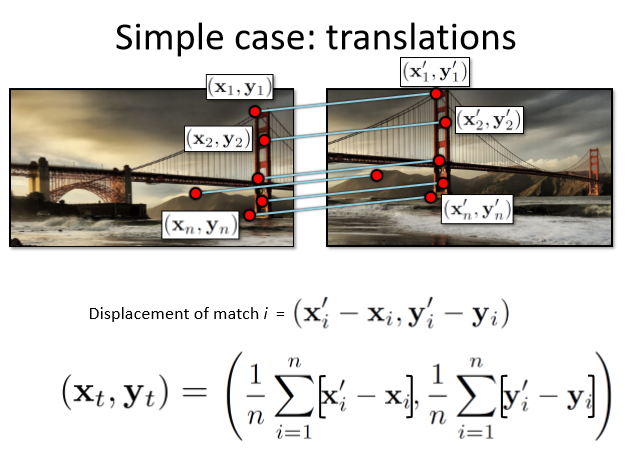
x`이 얼마나 이동했는지 x`-x를 통해 구할 수 있다.
이때 점들이 많고 각자의 변화량은 차이가 있을 수 있으므로 평균값을 통해 구한다.
translation의 xt, yt 즉, transformation matrix를 구하려면 각 이미지의 feature 1개의 변화량만 구하면 얻을 수 있다.
하지만 더 정확하게 얻기 위해 여러가지 feature를 구했고 이들의 변화량을 각각 구했다.
우리가 구하고자 하는 값은 xt, yt 2개 뿐이지만 방정식은 구하고자 하는 값보다 많은 상황이다
이러한 방정식 시스템을 Overdetermined system이라고 한다.
여러 개의 방정식으로부터 방정식의 해를 구하는 방법에 대해 알아보자
Least squares formulation
변화량이 적합한지 판단하는 척도로 Least squares formulation를 활용하려고 한다.
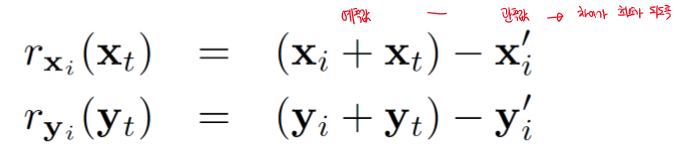
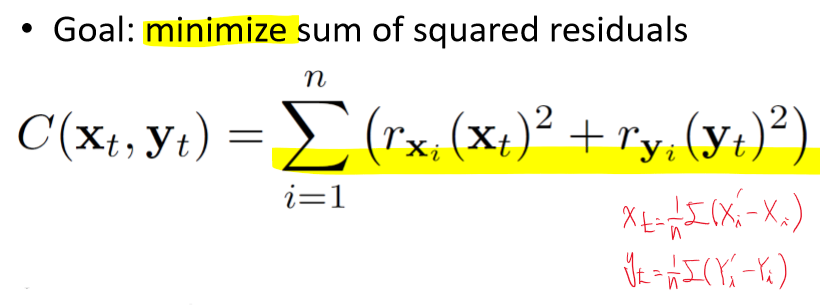
residual (편차)를 구해 그것의 제곱의 합이 가장 작아지는 것을 구하고자 한다.
위의 식을 행렬로 표현하면 아래와 같이 나타낼 수 있다.
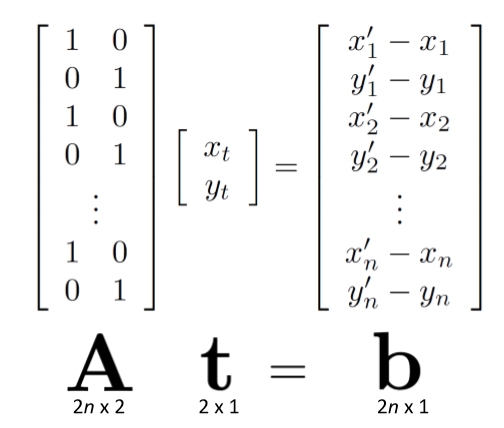
Lesat squares solution 구하기
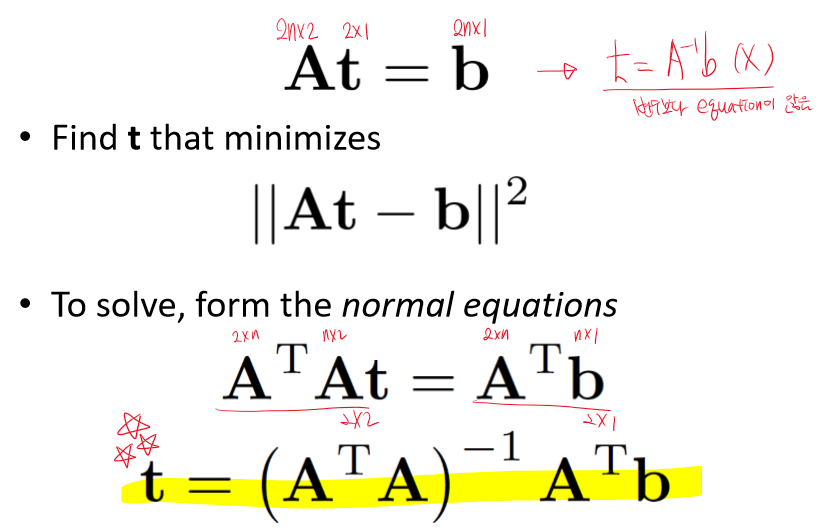
Affine transformation
위의 과정을 affine transformation으로 확장해보자.
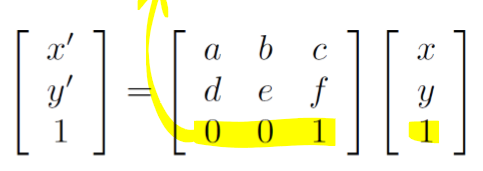
affine transform matrix는 마지막 행이 [ 0 0 1 ]인 것이 핵심이다.
matrix에서 필요한 변수는 6개이므로 최소 3개의 방정식이 필요하다.
하지만 translation matrix를 구했던 것과 같이 정확도를 위해 3개 이상의 방정식을 이용하여 해를 구하고자 한다.


Homographies
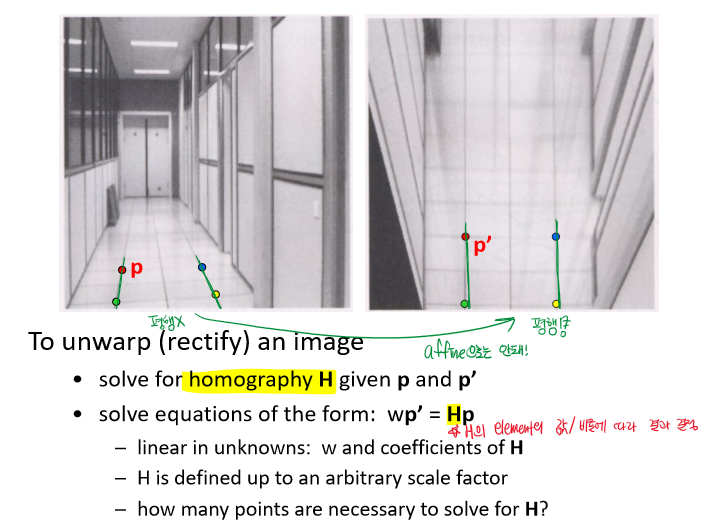
위와 같이 평행함이 바뀐 이미지는 affine transformation으로 해결할 수 없다.
Homographies matrix를 구하여 해결하고자 한다.
matrix에서 필요한 변수는 8개이므로 최소 4개의 방정식이 필요하다.
하지만 정확도를 위해 4개 이상의 방정식을 이용하여 해를 구하고자 한다.
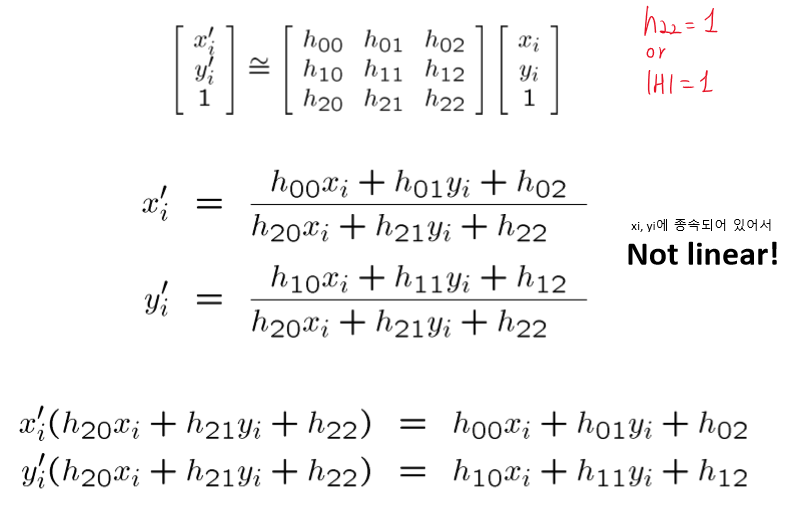
해를 구해보니 xi, yi에 종속되어 있어 liear하지 않다.
그래서 아래와 같은 형태로 바꾸어 계산하고자 한다.
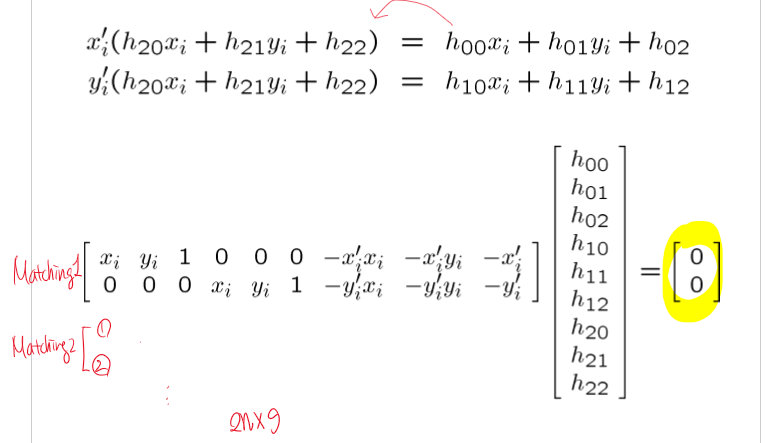

위에서 나타낸 식을 행렬식으로 나타내고 Ah - 0 식을 풀어냄으로써 해를 구할 수 있다.
이때 h는 scale에 종속되어 있어 결과 값으로 h의 unit vector를 구할 수 있다.
하지만 이때 zero vector 때문에 문제가 되는데
A의 transformation과 A를 곱한 값의 가장 작은 eigenvalue 를 통해 얻은 eigenvector로 h의 unit vector를 구할 수 있다.
정리

'Computer Science > 컴퓨터비전' 카테고리의 다른 글
| 컴퓨터비전:: RANSAC (0) | 2023.04.13 |
|---|---|
| 컴퓨터비전:: Transformation & Warping (0) | 2023.04.13 |
| 컴퓨터비전:: Image Descriptors & Match (0) | 2023.04.12 |
| 컴퓨터비전:: Harris corner detection (0) | 2023.04.12 |
| 컴퓨터비전:: Resample (0) | 2023.04.11 |
